How to represent the meaning of a word in computer
离散表示(discrete representation)
- 把单词作为一个个原子符号(atomic symbol)来表征:hotel, conference, walk…
- 对应到计算机中,使用独热编码(one-hot encoding)来存储:
[0 0 0 0 1 0 0 0] - 存在的问题:
1、向量规模过大:每个单词都对应一个单独的位,若要存储所有单词,则会需要一个非常大的向量。
2、难以计算单词间的相似性:这是一种localist representation, 每个one-hot representation是独立存在的,no inherent notion of similarity, 两两间并没有天然的相似性关系。
3、因此与其去研究an approach to work out similarity relationship between one-hot representations,不如直接探究an approach where representation of word encodes its meaning inherently,这样就能直观去计算单词间的similarity,这就是分布表示(distributed representation)的设计初衷。
注:这里的similarity指的是单词词义上的相似,而不是结构相似。
分布表示(distributed representation)
- 核心思想:通过单词的上下文(context)来理解词意。如
banking这个单词,我们让计算机知道经常和它一起出现的其他单词,就相当于明白了单词的用法——怎样将单词放到正确的上下文中,就相当于理解了单词的meaning。
- 具体方法:用向量定义词语的含义。通过调整一个单词及其上下文单词的向量,使得根据两个向量可以推测两个单词词义的相似度,就可以根据中心词向量预测上下文/根据上下文向量预测中心词。这就是我们常说的word2vec
遵循的基本原则:出现在相同上下文中的单词词义会相似。 - 注:区分distributed和distributional
distributed meaning:一种词义表示,和one-hot相对,one-hot将词义独立地存储在本地([0 0 0 0 1 0 0 0]向量中),distributed则存储在一个大的稠密的向量空间中。
distributional similarity:一种通过上下文来理解词义的方法,与denotational相对。
We use distributional similarity to build distributed meaning.
word2vec模型
Skip-grams(SG)
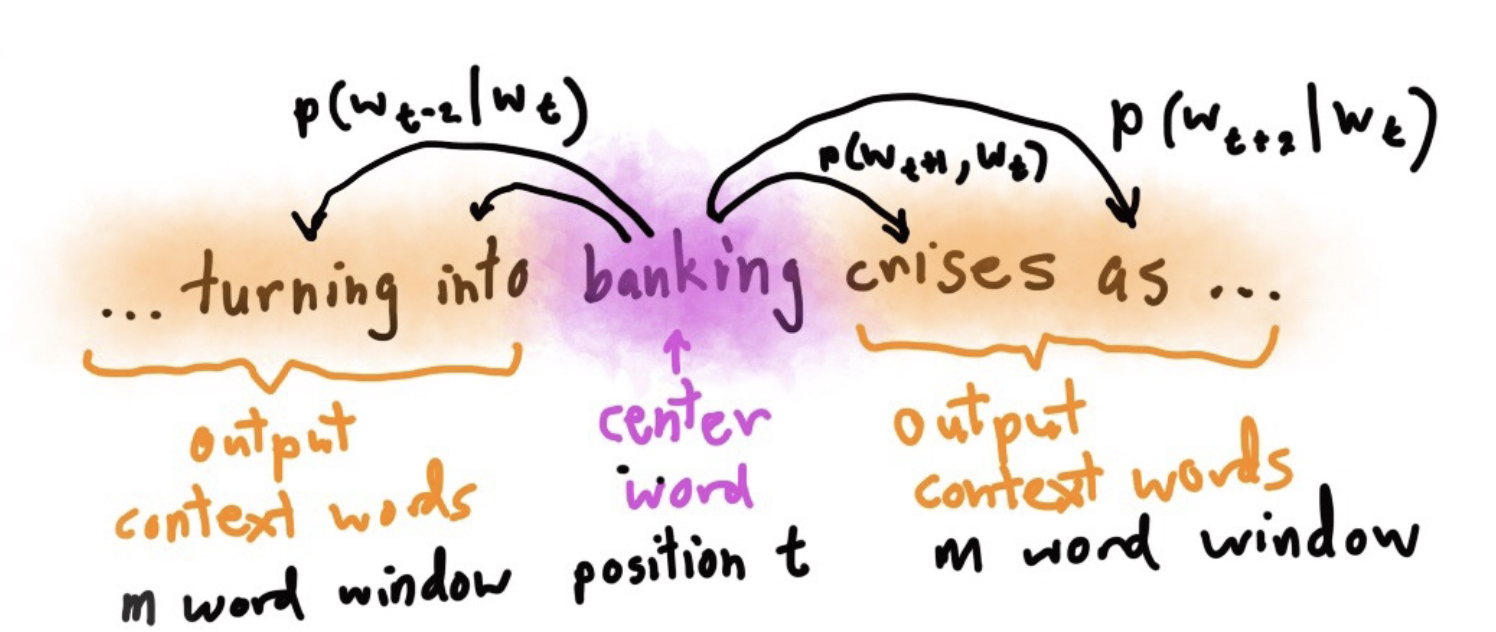
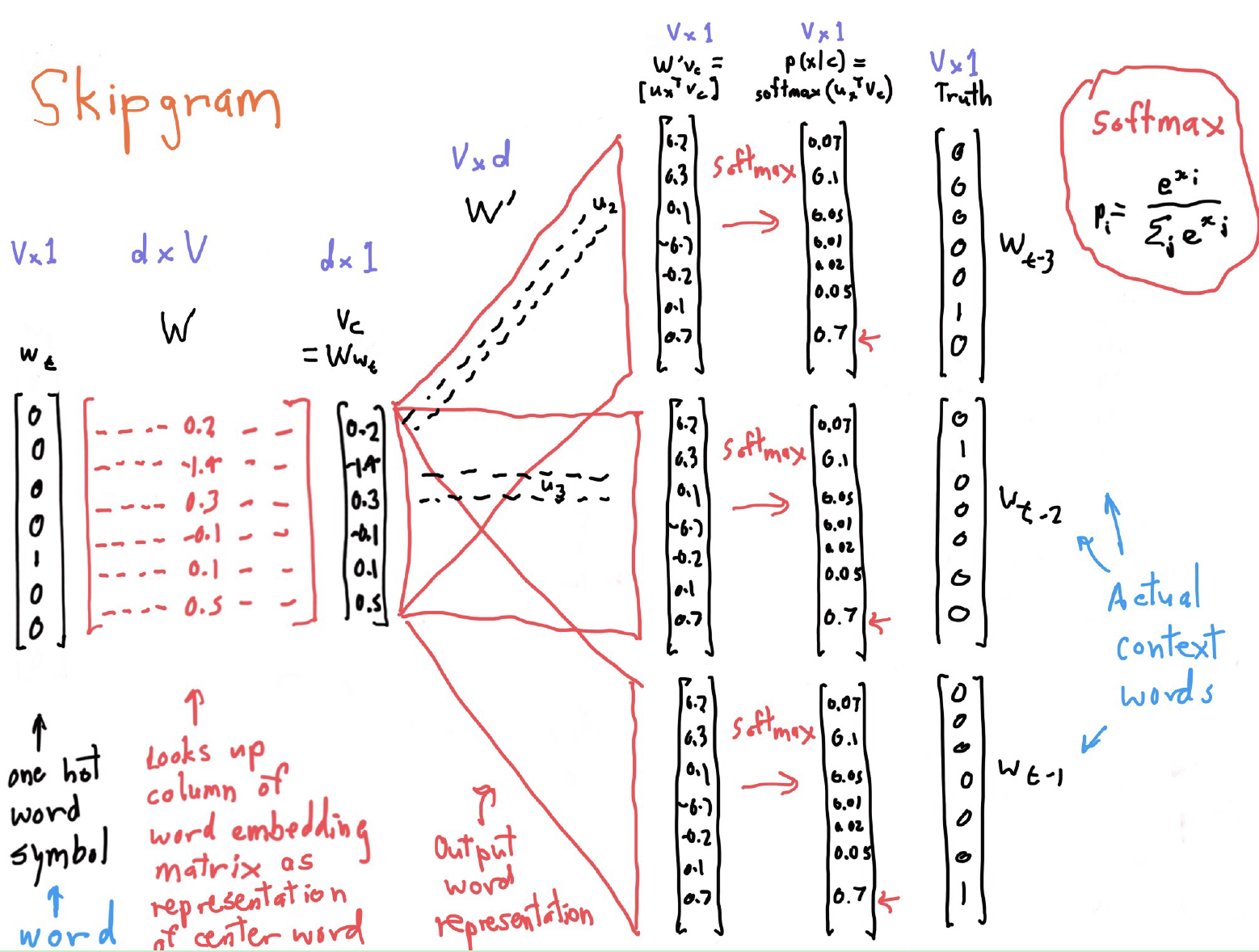
作用
通过中心词预测上下文。
定义预测单词上下文的模型
预测模型:\(p(context|w_t)\),表示在给定中心词\(w_t\)的条件下,正确预测出上下文单词的概率。
再具体点:\(p(w_{t-1}|w_t)\),\(p(w_{t-2}|w_t)\),\(p(w_{t+1}|w_t)\),\(t, t+1, t-1\)都是表示单词在文中出现的序号。
最终形式:
$$ p(w_{t+j}|w_t)=p(o|c)=\frac {exp(u_0^Tv_c)} {\sum_{w=1}^v exp(u_w^Tv_c)} $$
\(t, t+j\)是单词在文中的位置.
\(o, c\)则是单词在单词表中的序号,相当于在更为一般地表征两个单词的关联(与具体文本无关)。
\(v_c\)是中心词的词向量,\(u_0\)是上下文单词的词向量。
公式理解:首先是\(u_0^Tv_c\),这是一个点积操作,可用来粗糙地衡量单词间相似性(单词越相似,向量值越相近,乘积越大);其次是softmax操作,用来把值转换成概率:
$$\frac {exp(u_0^Tv_c)} {\sum_{w=1}^v exp(u_w^Tv_c)} $$
最终即得出了由中心词预测上下文单词的概率。
定义损失函数(Loss Function)
1、首先对模型全部相乘,表示文本整体的预测正确率:
$$ J^`(\theta)=\prod_{t=1}^T \prod_
{ \begin{align}
-m\le j \le m\\
j \neq 0
\end{align} }
p(w_{t+j}|w_t)$$
目标:整体正确率最大,maximize the function,
2、做Negtive Log Likelihood处理,使maximize->minimize,即得到最终的损失函数。
$$ J(\theta)=-\frac {1}{T} \sum_{t=1}^T \sum_
{ \begin{align}
-m& \le j \le m\\
j \neq 0
\end{align} }
p(w_{t+j}|w_t)\\
p(w_{t+j}|w_t)=\frac {exp(u_0^Tv_c)} {\sum_{w=1}^v exp(u_w^Tv_c)}
$$
最终目标:使损失函数最小。
怎样求损失函数最小值:梯度下降(gradient descent)
注1:具体求解过程见lecture slide。
注2:求梯度时对\(u_o和v_c\)都要求偏导,最后组合成梯度向量。且求的是向量的导数,和实数求偏导有一定区别。
注3:当数据量过大时,可使用SGD随机梯度下降来加快速度(一个窗口计算一次梯度,用来估计整体梯度)。
怎样训练模型
模型中的参数就是每个单词对应的word vector向量,将所有参数组合成一个的大向量\(\theta\),即作为损失函数的自变量。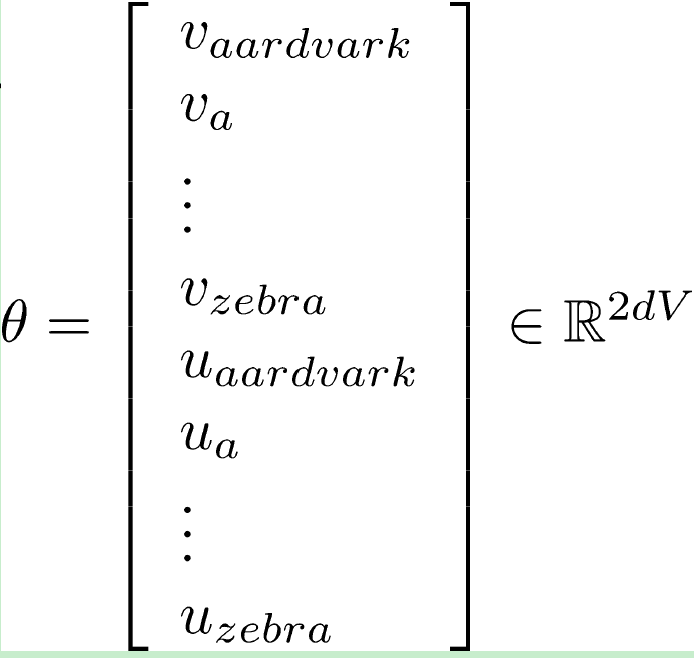
总共V个单词,每个单词对应两个词向量,词向量每个d维,因此\(\theta\)总长度为2dV。
为何每个单词对应两个词向量:作为中心词时一个,作为上下文单词时一个,这样更方便数学处理。
Continuous Bag of Words(CBOW)
作用
通过上下文预测中心词
To be continued
遗留问题:
- SG模型中,计算每个上下文词向量的值时,context matrix是一样的? 那计算出的结果不就一样了?————context matrix是一样的,但因为每个单词的词向量表征是不一样的,所以最终训练出来的上下文词向量也是不一样的。直观来说,context martrix是一各由中心词->上下文的转换, 在词向量空间中从一个单词向这个单词周围来扩展(词义相近单词离得近), 这种变化对每个单词都是一样的, 因此context martrix一样也是正常的.
- 如何迭代\(\theta\)来更新梯度?把\(\theta\)初始化成什么样子?
————按照梯度下降的法则来更新参数; 参数初始化有多种策略. - 这是有监督的学习过程,损失函数中没有出现计算误差的部分?
Post Date: 2018-11-05
版权声明: 本文为原创文章,转载请注明出处